Samuel

Introduction

Pipes add detail and realism to 3D scenes, yet they are tedious to model manually and adapting them to scene changes is difficult. But thanks to the power of Blenders geometry nodes system, tasks like these can be automated with ease. In this blog post I will explain the concepts behind my pipe generator in detail. Bear in mind that I can't explain every step down to the individual node or this post would turn into a novel, and I'd rather use that time to work on other Blender projects. The post covers how to turn basic edges into pipes, how the automatic path finding works, what to consider when adding random offsets and finally I'll explain the hacky way I used to add junctions.

Water to wine, edges to pipes

Lets start with the basics: we need a node group that can turn any input edge into a pipe. Once we have this set up, we can later build upon it by adding the fancy stuff like path finding and special treatments for junctions.

The first thing to consider is the rounded curves. No pipe has straight corners, so we need to find a way to fillet them. Luckily there is a curve node that does just what we need: “Fillet Curve”. But we only want to fillet the corners, so we have to check whether the two edges are parallel to each other or not. This is where your vector math knowledge from school will come in handy: we're using the dot product of both edge directions. If the dot product is 1, the vectors are in a 90° angle to each other, if its 0, they're parallel. Use the “Field at index” position of the current index, the index -1 and the index +1 to find the edge directions.

Once this is done, there's two steps left for a basic pipe: turning it into a 3D mesh and adding the flanges. The first step is easy: simply use “Curve to Mesh” with a curve circle as profile. Adding the flanges is a bit harder. How do we determine on which points of the curve to instance the flanges? There might be better ways, but I did it with the “Attribute Statistics” node, using the edge length as input. We can assume that the tiny edges added by the filleting step are the shortest edges of the pipe, as well as the most common length statistically. We don't want to instance on those filleted corner vertices, just on the rest. So we create a selection where every edge larger than the median length is considered for flange instancing (for which we can use the “Instance on Points” node). On top of that we then add every vertex to the selection that has only 1 adjacent vertex. Why? Because we want the start and end points of our pipe to get flanges too.

How do we find the right direction in which to rotate the flanges? Easy, by capturing the curve tangent of the input edges and passing them to the “Rotate Instances” node via an “Align to Euler” node.

From 3D lettuce lattice to path

Now that we have a node group that turns every edge we throw at it into a pipe, it's time to start with the cool stuff: letting the math do the work for us.

If we want to create orthogonal paths that follow our input edges, we could use the “Shortest Edge Path” node. In conjunction with the “Edge Paths to Curves” node, we can pass selections for the end vertex and the start vertices to the path finding algorithm, which then tries to find a path through a mesh to connect these vertices, taking into account arbitrary edge cost values. That leaves us with two questions: how do we create a 3D lattice mesh around our input edges which the Shortest Edge Paths node can work in, and what do we use as edge cost?

To create a 3D edge lattice (there's plenty tutorials about that on YouTube) we simply create a 2D grid with the given X and Y dimensions and duplicate it upwards along the Z axis. The amount of subdivisions and duplications along the Z axis depend on the lattice resolution we need; I created a parameter that controls this resolution. As a last step for a basic 3D lattice we need the vertical edges: we instance upward-pointing curve lines on every vertex of the bottom-most grid, and divide the curve lines by the amount of grid rows on the Z axis. This subdivision step is required so we can use the “Merge by Distance” afterwards, which merges all vertices together.

Now that we have a generic 3D lattice, lets make it adapt to our input geometry. To do that, we use the “Convex Hull” node on our input geometry; it creates an enclosing mesh around all our input edges. We can then use the statistics of the positions of the convex hull vertices to change the scale of our 3D lattice and its offset in 3D space (otherwise we'd end up with a lattice that stays the same whatever we use as input geometry). For that we use the Range and Minimum values of the Attribute Statistic node.

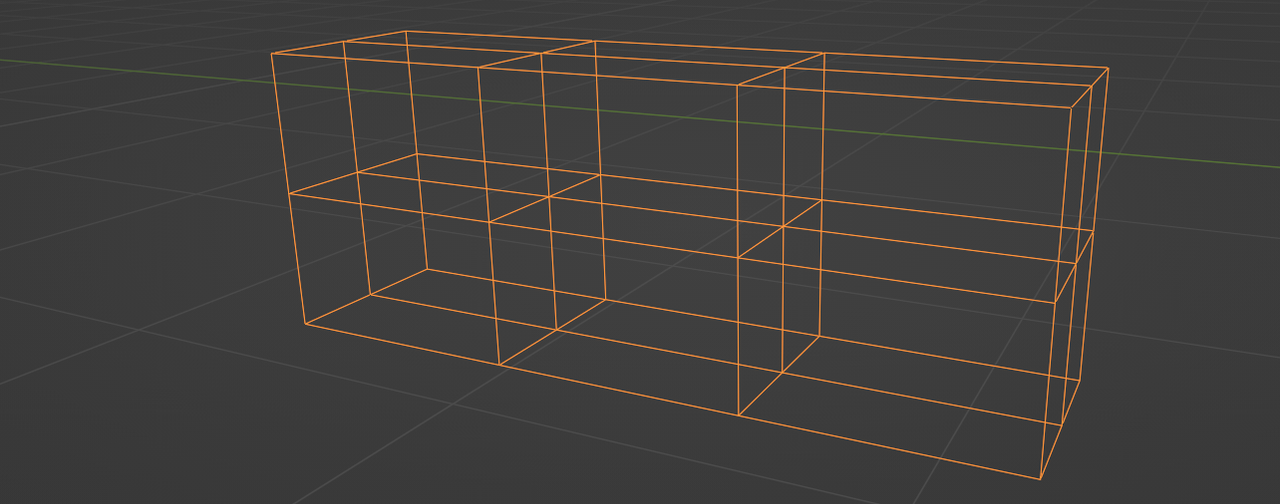
To break the repetitive pattern of the lattice, we should offset the edges in random directions. But what happens if you offset a single edge of the lattice in a random direction? The adjacent edges won't be orthogonal anymore. To fix this, we have to move every row of each dimension as a whole. That means every edge in the X-Y plane would have to move in a random Z direction. To get a random value per row, we can use a noise texture with a one-dimensional vector as its input vector. Lets take the X dimension as an example. Our noise texture will only change in [1, 0, 0] space. We do the same for the other dimensions and combine them to a unified vector value (because its easier to pass on). We then capture this vector for every point on the lattice and let it drive the offset of the “Set Position” node. And et voilà, our lattice is no longer repetitive.

Time to move on to the Shortest Edge Path. How do we tell the path finding algorithm where to start and to end and where to draw the paths? To do that, we transfer the positions of our input edge start- and endpoints with the position of the “Sample Index” node to the “Sample Nearest” node that takes these positions and transfer them to the 3D lattice as its input geometry. The resulting selection contains the nearest vertices in the 3D lattice corresponding to our input edge start- and endpoints. And the edge cost? We simply use the distance value of the “Geometry Proximity” node to drive the edge cost. The farther a lattice edge is from the input edge, the less likely it is to be used by the path finding algorithm.

Junctions

What's left? I'm not a plumber, but I think whenever a pipe splits up into two sections, there needs to be a junction piece. How could we add this to our existing node graph? We already have a group that adds flanges at the end vertices of edges, so why not use that to our advantage?

First we have to select all junction vertices. Those can be found by checking how many vertex neighbours each vertex has. The most elegant way would then be to spawn N lines on each junction vertex, where N is the number of adjacent junction edges, and then capture the directions of said junction edges and rotate the instanced lines accordingly. I tried that ... and it didn't work, because I couldn't find a way to tell the node gods which rotation belongs to which instanced line; their indices are completely different from the indices of the junction edges.

So back to the scratch pad we go. What if we simply create a 6-way hedgehog of lines (one in each orthogonal direction; +/-X, +/-Y, +/-Z) on every junction vertex and then delete those of the lines that don't overlap with the pipe? Using the distance of the Geometry Proximity node, we can drive a Compare node and create a selection. Each of the hedgehog lines (what a silly name) whose distance is bigger than close to zero gets deleted. What remains are lines that align with our existing pipe paths and have a defined distance to our junction vertices. Of course this only works as long as the paths are orthogonal to each other, but its better than no junctions at all, I guess.

Conclusion

So there you have it, this is how I created my pipe generator. I had to cut a lot of corners in my explanation (or should I say, filleted?) but I hope you get the general idea of what's going on and could learn a thing or two about working with Geometry Nodes. If you want to try out the generator yourself or dissect my node graph, you can grab it here on Blendermarket for a few bucks. Happy blendering!