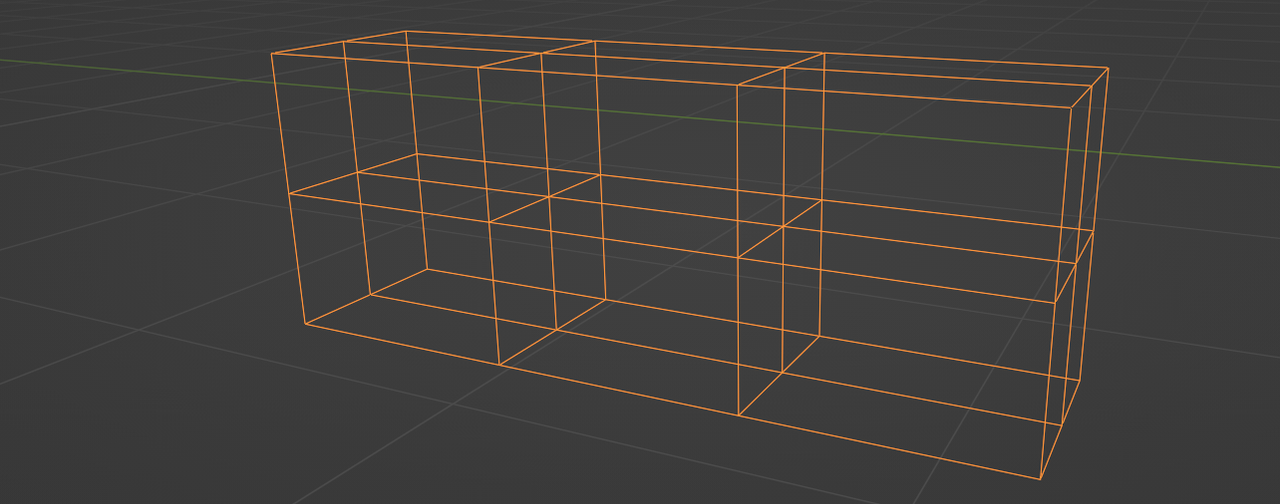
Blender Scaffolding generator from scratch

0. Introduction
This blog post explains the main principles behind my recently released Scaffolding Generator. You can find a showcase video of it here on my Peertube channel. Due to the sheer number of nodes involved, I won't be able to explain everything to the finest detail. However, I still want to give you a broad overview of my thought process and how things work.
The base idea of the generator is simple. We feed it mesh edges, which are easy to move around and extrude, and out comes a scaffold. We want it to be able to adapt to corners. There should also be input parameters for the amount of floors, for their height and for the depth of the scaffold. With these inputs, we can control the generator from the modifiers tab without having to poke around in the geometry nodes graph. The scaffold should consist of floors (obviously) and of poles that connect everything in all three dimensions. Once that is figured out, we can move on to ladders and barriers and any other unnecessary detail that comes to mind.
When solving out complex problems like these, it is important to break them down into smaller and smaller problems until you can solve them bit by bit, but still keep the big picture in mind. So let's start building from the bottom up.
1. Creating a base floor
Scaffoldings are repetitive, so it makes sense to start with the most basic structure: a single floor. Our goal is to turn turn the input edges into a plane with parallel sides that resemble a floor.

There's an easy way to extrude curves, and it's called “curve to mesh”. That means we first need to convert the input edges by using the “Mesh to Curves” modifier. Then all we have to use as the extrusion profile is a curve line that is rotated orthogonally to the direction of the input curve. The length of the profile curve corresponds to the width of our scaffold.

The result looks promising already. However, we can see that it messed up the corners; this is because the profile curve has been rotated by 45° at that point and not scaled accordingly. Thus, the extrusion ends up being too thin. Luckily for us there is a relatively easy fix for this, at least for angles between 90-180° (which is what we are interested in; most scaffoldings have >90° angles). You are free to dive down the rabbit hole by following this great tutorial by Blender Bash, but I will show an easier way here.
Since we're dealing with a curve as input, we can take advantage of the “set curve radius” node to scale every point of the curve according to the angle of its adjacent edges. Make sure to set the curve radius prior to doing the extrusion operation or this will not work. To access the angle between two curve segments, all we need to do is to calculate the dot product of its vectors like so:

Now let's use this dot product to adjust the curve radius. Remember, the absolute value of the dot product equals 0 for 90° angles and 1 for 180° angles. The base radius at every point along the curve is 1, and the adjusted radius at a 90° angle should equal 1.414. The keen reader will recognize this number, its the square root of 2. Assume a right triangle where the two adjacent sides are of length 1. Using good ol' Pythagoras, the length of the hypothenuse then equals the square root of 2 (or the sum of both sides squared). We could also go the accurate route and implement the following formula:
angle = acos(dot_product)
radius_adjustment = 1 / cos(angle / 2)
The easier but slightly inaccurate route, which I took, because I am lazy, is to use a Map Range node that turns the range 0 to 1 into a range of 1.414 to 1. Its a linear interpolation, but its close enough (and nobody will notice anyway).
To prevent the endpoints of the curve from being affected by this operation, simply run the radius adjustment through a Switch node with an Endpoint Selection as toggle. If a point either belongs to start or end, set the radius to 1. And that is how to adjust the radius at each point to create a (somewhat) even extrusion of our base floor.
2. Up we go
The base floor we just created will help us in two ways: 1) we can use it as actual floors if we manage to duplicate it upwards along the Z axis, and 2) we can extrude it to create the geometry that will later be turned into poles. Using our “Floor height” input parameter as the offset scale of the “Extrude Mesh” node, we can achieve something like this:

An easy way of creating arrays in geometry nodes is the Duplicate Elements node. We pass our number of floors into its Amount socket, und use the provided Duplicate Index to drive the offset. The Duplicate Elements node can work on any domain (points, edges, faces, etc), but here I chose the Instance domain. That means we first have to convert the incoming geometry into an instance. Because of this, we are then able to use “Translate Instances” with the Duplicate Index being responsible for the upwards translation. Multiply this with the Floor Height and we got ourselves a group that creates arrays along the Z axis:

Make sure to package these nodes into a group so we can then later repeat the process with other geometry (like the ladders).
Time to turn our first prototype into poles. Same as with the ground floor, we use the “Curve to Mesh” modifier, but this time with a small curve circle as the profile. It's a good idea to wrap these nodes into their own group to re-use them for the ladders (I will call it the solidify group). Don't forget to turn your mesh into curves before the extrusion. The result should look like this:

3. Adding cuts
We can see that we need to add sections to our scaffold. Right now there are no subdivisions: the poles become as long as the base curve, and that's not really how scaffolds work. Time to move back to the early stages of our generator where we only have to deal with a few simple base curves. There is a “Subdivide Curve” modifier that allows us to set the amount of cuts we want to place inside a single curve. Right now, all the base curve segments are connected as a single curve, which means any cuts that we perform will be applied to the base curve as a whole. To treat every segment separately, we have to use “Split Edges” first, before our input edges are turned into the base curve. After splitting the edges, we capture an integer attribute that will control the amount of cuts. This attribute is calculated as follows:
- We first calculate the total length of each segment using the “Edge Vertices” positions, subtracting them from each other and calculating their length with a vector math node
- This length is then divided by a “Section length” input parameter that controls how long each section should be
- We floor the resulting value so that new cuts only spawn once a full section length is reached
If we now subdivide the curves according to our captured attribute, we will notice that they are not connected anymore; the extrusion operation will create two separate floor parts. That means we have to reconnect all individual curve segments that we split earlier. To do that, we turn our curve into a mesh again so that we can use the “Merge by Distance” modifier. As final step, we convert the merged mesh back into a curve. To summarize, the nodes will look like this:

4. Ladders
Okay, this part is going to be node so easy (I am not sorry). Let's first think about where we want to place ladders. We don't want to have ladders in every segment of our scaffold, but they should be placed in a regular distance along the base curve. That means we have to tell every segment of our base curve (after we subdivided it in section 3) whether or not a ladder should be placed on that position or not.
We can use the base curve to spawn ladders because of the “Mesh to Points” modifier, set to Edges. This modifier replaces all incoming edges with a point, on which we can then instance our ladders. And because “Instance on Points” allows us to pass it a selection as a Boolean value, we can store a Boolean attribute for each of the base edge to tell it whether a ladder should be spawned there or not. We do that after we subdivided our base curves and turned them into a mesh (aka edges) again. I call this attribute is_ladder. To get a repeating selection, we pass the Index of our edges into a modulo operation (for example with a modulo of 3), and compare the result with an integer (like 0). The result is a Boolean selection that is true for every third segment of our base curve.
Next comes the actual ladder. It should consist of two vertical poles, connected by a number of rungs. The height of the ladder should adapt to the floor height, and the amount of rungs should also adapt accordingly. The ladder should be tilted in an alternating pattern and spawn on every floor except for the topmost one. For the ladders we can re-use our solidify group to turn the curves into geometry. I can't explain every little detail of the ladder nodes here or this tutorial would never end, so let me try to summarize the steps:
- Create a single vertical curve line and set the X values of its start and end positions so that it is slightly tilted and adapts to the section length (the smaller the section length, the less the ladder is tilted).
- Resample the curve line based on the floor height (using a couple of math nodes).
- The created points of the curve can then be used to instance rungs (again just curve lines).
- Using our initial vertical curve line, we move it left and right by half the rung width to create the side poles of the ladder (and we join it with our instanced rungs).
- The resulting ladder consists only of curves for now, so we can scale it along the Y axis to adapt it to the width of our scaffold.
- Solidify the ladder curves to actual poles, using the solidify group we created earlier
- Stack the ladders using our floor stacking group (with the count being one less than the total floor count). The result is a single vertical stack of ladders.
- Every second of the resulting ladder instances is then rotated by 180°, driven by a
floor_indexattribute that needs to be captured for every instance of the stacked ladders (inside our stacking group). - After realizing the ladder instances, we can then instance the whole ladder stack on every point of our base curve (with the
is_ladderselection applied). - To rotate the ladder stacks according to the base curve, we need to store a curve tangent value for every base curve segment and pass it through an “Align Euler to Vector” node.
The result of our effort will look something like this:

5. Drawing the rest of the owl
There is certainly a lot more that can be done to further improve our little generator. However, I won't go into too much detail here anymore because most of the basic principles have been covered extensively, and many of the remaining details simply repeat the processes I've described earlier.
One of the more important aspects yet to do is to add those small outer offsets of the poles. Remember when we turned the mesh into curves that later became our poles? We can offset the start- and endpoints of these curves (separately) with the “Set Position” node with the help of the curve tangent attribute. The tangent is the vector that aligns with the direction of the curve. All we have to do is to normalize this tangent, so we don't end up with differently sized offsets, and use it as the offset of our “Set Position” node. You can then change the amount of offset by multiplying it with a small value.
Some scaffolds have diagonal poles in addition to the normal poles. We can create these using the “Triangulate” modifier. This operation must be performed on faces, i. e. right after we have extruded and stacked our floors.
To add barriers to the endpoints of our scaffold, we can again first create a single barrier object by manipulating curves (as we did with the ladders), solidify it with our solidify group, then stack it and instance these stacks on the endpoints of our base curve.
To add connector pieces where the poles intersect, we simple craft a little connector object with a small cylinder and a few extrusion and scaling operators, and then instance it on the vertices of the our stacked pole geometry. This should be done before we add the outer offsets of our poles, because we don't want to add the connectors at the very endpoints of our poles if they have offsets. We rotate the connectors according to the curve tangent.
And last but not least, we can offset each pole so that it won't intersect with its adjacent poles. It will look like the poles actually overlap each other instead of being directly connected. To offset each pole with a “Set Position” node, we first have to find a way to create a unique offset direction (or vector) for each pole curve. For this, I came up with a neat little idea: we create the cross product of two vectors, one being the face normal (the direction pointing away from the scaffold) and the other one being the curve tangent. The resulting vector points in a direction orthogonal to both of the other vectors. We capture the face normal and the curve tangent attributes with a “Capture Attribute” node set to the face and the point domains respectively. Bear in mind that the face normal needs to be captured before our extruded pole geometry is being turned into curves, i. e. while it still has face data. The captured vectors then need to be run through a Normalize and an Absolute step before being turned into the cross product.
I added a few more details like feet (simply instanced on the vertices of our base floor) and side panels (extrusions of the base floor with deleted upper and lower faces). The result looks like this:

And here is my abomination of a node graph:

6. Wrapping up
Well that was quite the ride, wasn't it? We started out with a single curve. We extruded it to form a base floor and fixed the corner width with completely inaccurate math tweaks. We extruded the base floor to generator pole geometry, which we then stacked to get a basic scaffold shape. We added diagonals and ladders and solidified everything to turn it into poles. At the end we merged our different branches of geometry together.
Thank you for taking the time to read my blog post to the end and I hope you learned a few things here and there. I am sure there exist smarter ways to do many of these operations, so hit me up on Mastodon with your thoughts and ideas. Critique and feedback is always welcome.
And now I wish you happy blendering!